2 Stress
Introduction
Click to expand
Having reviewed static equilibrium in Chapter 1, we now know how to find the internal loads in a body using equilibrium. When determining whether a body can resist the loads applied to it, the internal load is only part of the solution. The dimensions of the body and the inherent properties of the material it is made from are also important.
In this chapter we’ll explore the concept of stress, which can help us determine whether an object will physically break when subjected to a load. We’ll cover average normal stress (stress perpendicular to the cross-section) in Section 2.1 and average shear stress (stress parallel to the cross-section) in Section 2.2. We’ll then discuss bearing stress (the stress between two bodies in contact with each other) in Section 2.3 and finish with the average normal and shear stresses on an inclined cross-section in Section 2.4.
2.1 Average Normal Stress
Click to expand
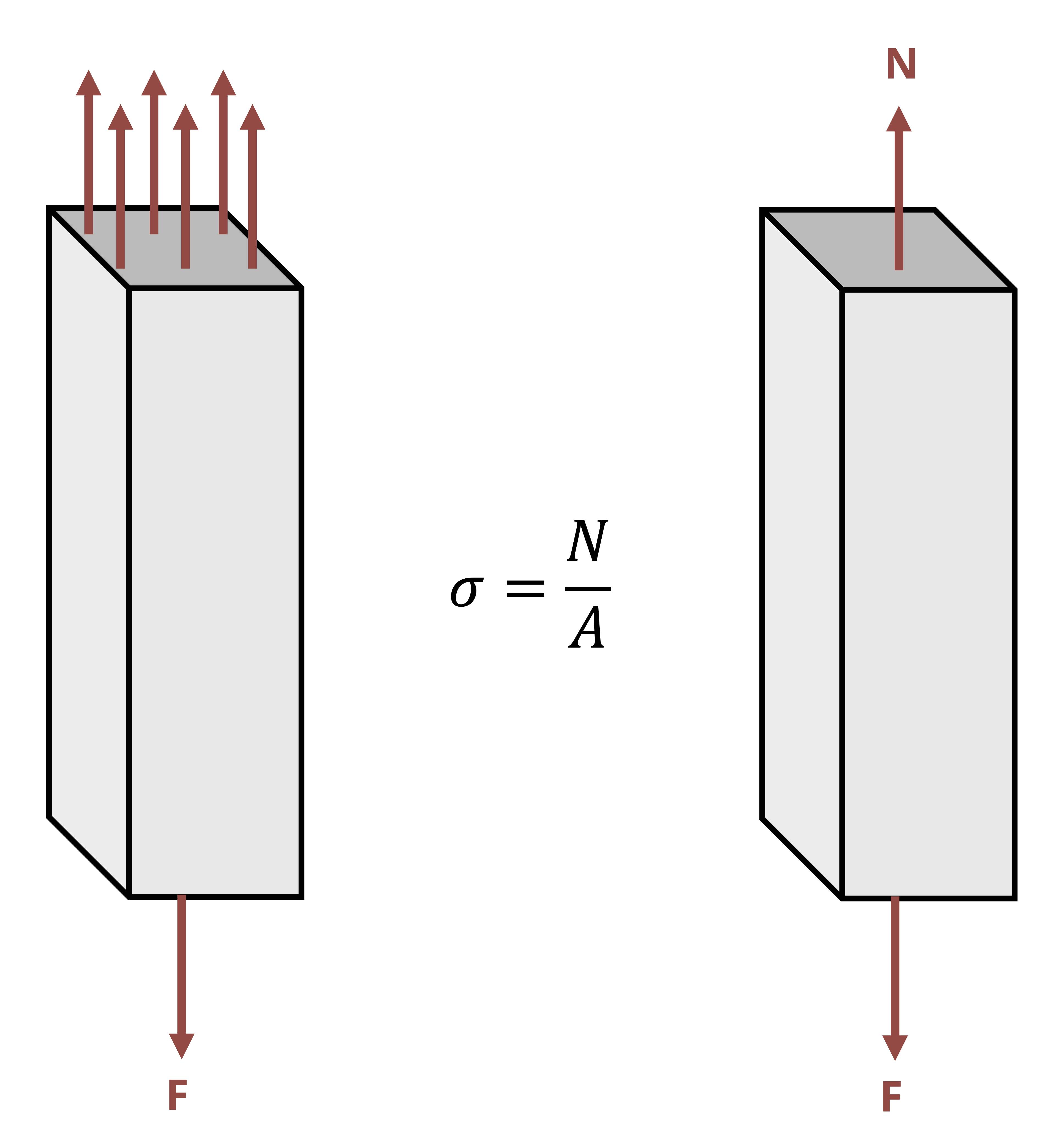
Average normal stress is defined as the internal normal force divided by the cross-sectional area of the body. It is given the Greek letter sigma (σ). Stress increases as the force increases or as the cross-sectional area decreases.
\[ \boxed {\sigma=\frac{N}{A}} \tag{2.1}\]
𝜎 = Average normal stress [Pa, psi]
N = Internal normal force [N, lb]
A = Cross-sectional area [m2, in.2]
As such the SI units of stress are N/m2, more commonly referred to as the Pascal (Pa) where 1 Pa = 1 N/m2. The US customary units for stress are lb/in2, commonly written as psi. Since stresses can get very large, it is common to use prefixes such as kilo (k) and mega (M) to represent 103 and 106 respectively. A stress of 15,000,000 Pa is written as 15 MPa. A stress of 35,000 psi is written as 35 ksi.
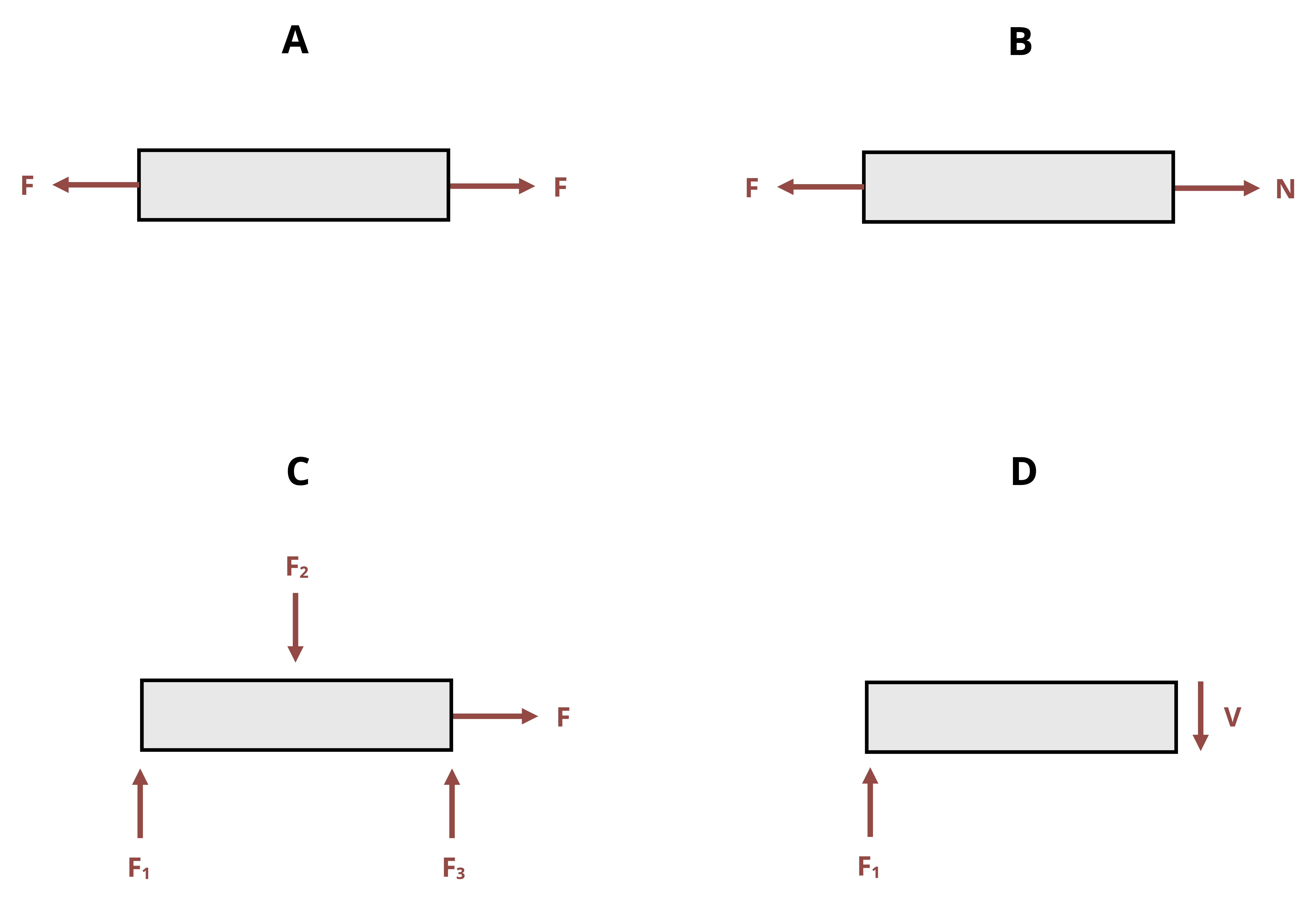
Normal stress occurs perpendicular to the cross-section and so is associated with either a pulling or pushing motion (Figure 2.1). Normal forces that pull on a cross-section are known as tensile forces and create a tensile normal stress. Normal forces that push on a cross-section are known as compressive forces and create a compressive normal stress. The normal stress calculated above is really an average normal stress as the force is distributed over the cross-section, but we generally simplify this to a concentrated force that creates the same normal stress at every point on the cross-section (Figure 2.2).
The internal normal force in a body can be found through the method of equilibrium as reviewed in Section 1.2. See Example 2.1 for a demonstration.
Sometimes the loading or cross-sectional area of the body will change, resulting in a change in stress. In these cases the stress can be calculated separately in each segment of the body by first finding the internal load in each segment and then dividing the internal load by the cross-sectional area of the respective segment. Different parts of the body may experience different stresses. Generally the highest stress is of most importance as that is the stress that typically determines whether the body will break. Because we do not know in advance where the largest stress is, however, it is typically necessary to calculate the stress at each different cross-section in order to determine the highest stress. See Example 2.2 for a demonstration.
2.2 Average Shear Stress
Click to expand
Average shear stress is defined as the internal shear force divided by the cross-sectional area of the body. While normal forces (and therefore normal stresses) occur when a body is under tension or compression, shear forces (and therefore shear stresses) occur when a force is tangentially applied parallel to the cross-section, resulting in a sliding motion (Figure 2.3).
Although the basic definition of average normal stress and average shear stress is the same (force divided by area) there are some differences. To quickly differentiate which stress we are talking about, shear stress is denoted by the Greek letter tau (τ).
\[ \boxed{\tau=\frac{V}{A}} \tag{2.2}\]
τ = Average shear stress [Pa, psi]
V = Internal shear force [N, lb]
A = Cross-sectional area [m2, in.2]
Like normal force, internal shear force can be found by cutting a cross-section through the body, drawing a free body diagram, and applying equilibrium equations. See Example 2.3 for a demonstration.
Shear stresses are common in both members of a structure and also in the fasteners between members. Depending on how these connections are formed we may see multiple shear planes. It is very important to correctly identify the internal force in the body. Figure 2.4 demonstrates the difference between single and double shear configurations for a pinned joint and the effects on internal shear force. See Example 2.4 for an example where double shear occurs.
2.3 Bearing Stress
Click to expand
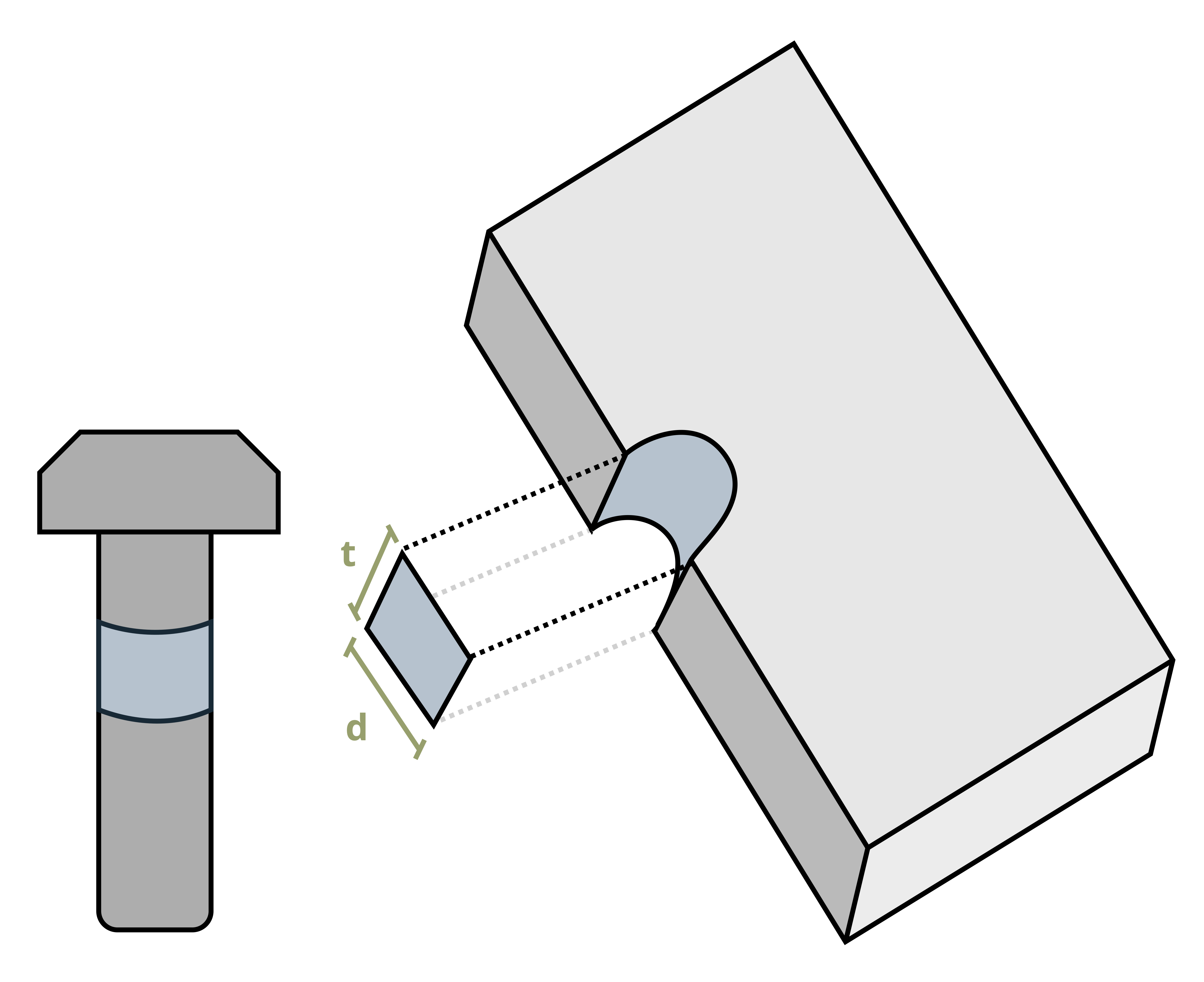
Bearing stress is similar to normal stress, except that it occurs at the contact area between two bodies instead of within a single body. Bearing stress is calculated with the average normal stress equation, where the cross-sectional area is the contact area between the two bodies (Figure 2.5).

One common situation is contact between two curved edges, such as the bolt in Figure 2.6. In this situation it is common to use the projected contact area between the curved surfaces, which forms a rectangle of base d and height t. This greatly simplifies the calculation, but again represents an average value for the contact or bearing stress.
2.4 Stress on an Inclined Plane
Click to expand
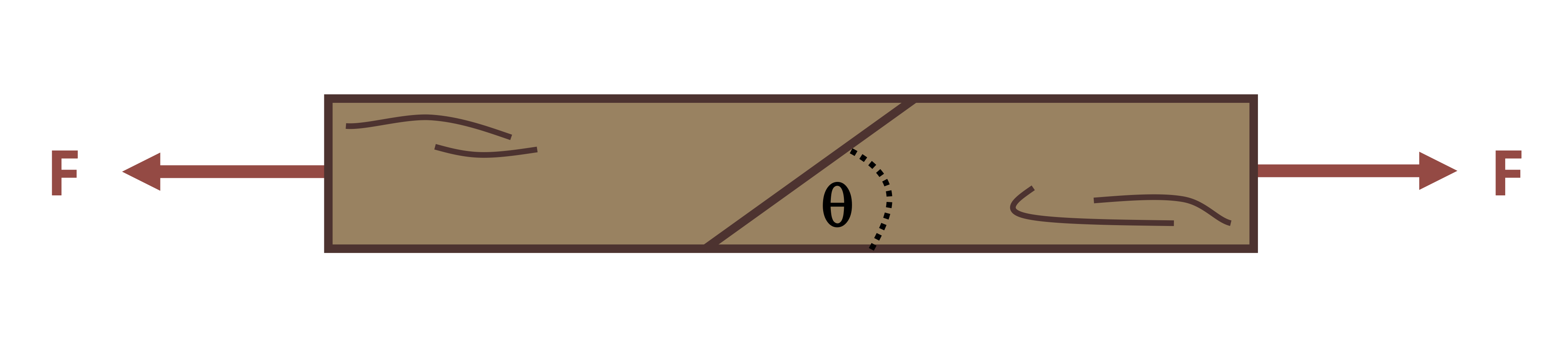
We have so far been cutting cross-sections perpendicular to the external force, or parallel to it. However, there is no rule that says we have to do this. It is perfectly acceptable to cut cross-sections at an angle and there are many situations where it may make sense to do so (Figure 2.7).
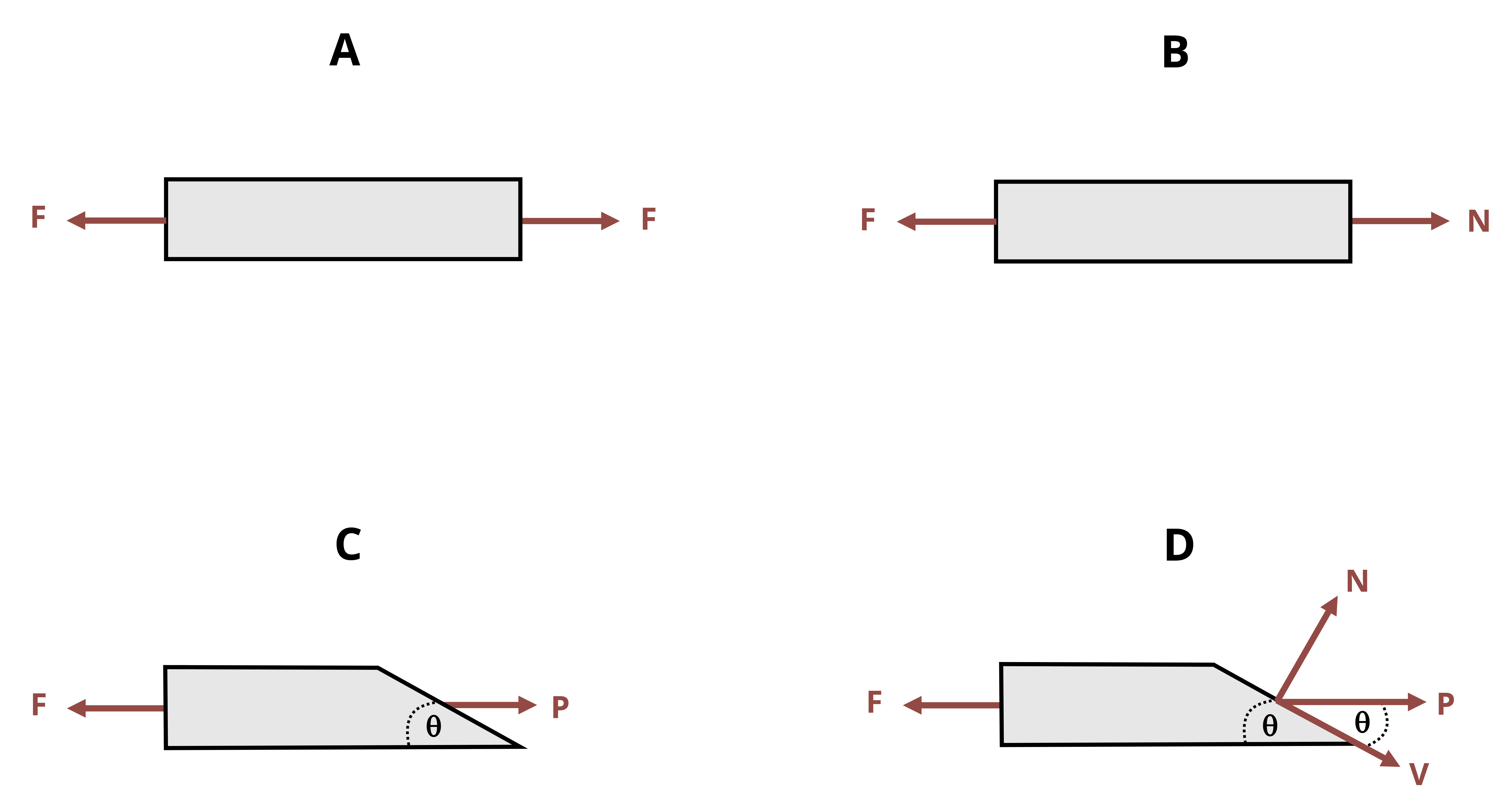
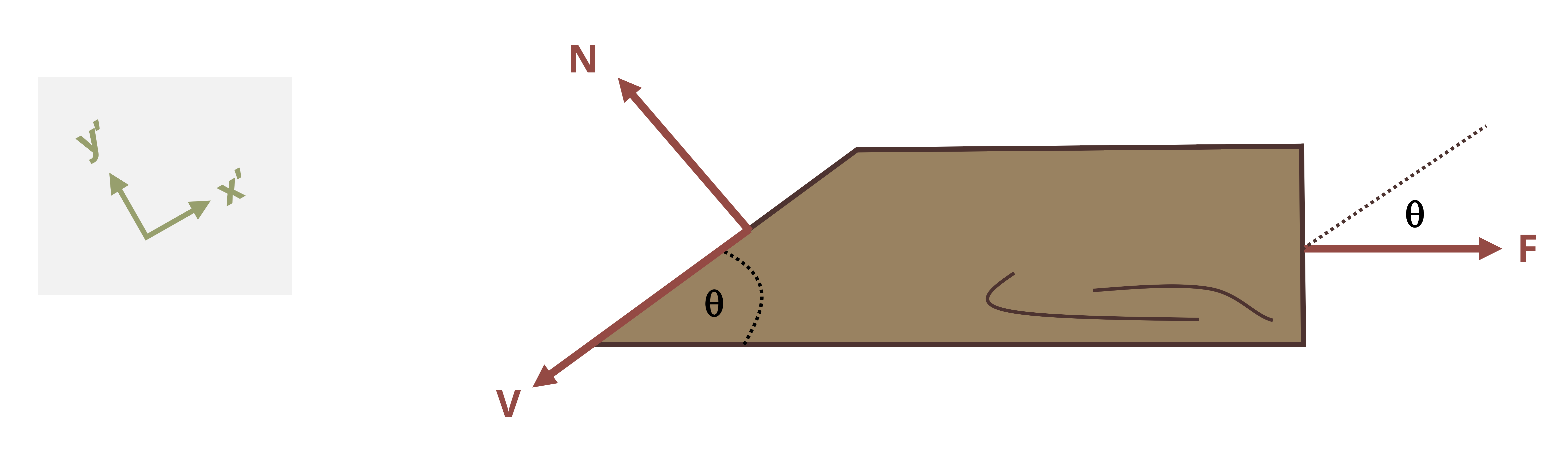
In this scenario the internal load must still be equal and opposite to the external load in order to maintain equilibrium but, because we cut the cross-section at an angle, this internal load is neither parallel nor perpendicular to the cross-section. Therefore it is not entirely a normal force or a shear force. However, the internal force may be broken into components that are perpendicular and parallel to the cross-section.
\[ \begin{aligned} & N=P \sin (\theta) \\ & V=P \cos (\theta) \end{aligned} \]
The area used to calculate the average normal and shear stresses must be the area of the inclined plane (Figure 2.8). By setting up a right-angled triangle it should be apparent that the area of the plane, Ap, can be found from:
\[ A_p=\frac{A}{\sin (\theta)} \]
We can calculate average normal stress from:
\[\boxed{\sigma=\frac{N}{A_p}=\frac{P \sin (\theta)}{\frac{A}{\sin (\theta)}}=\frac{P \sin ^2(\theta)}{A}} \tag{2.3}\]
We can calculate average shear stress from:
\[\boxed{\tau=\frac{V}{A_p}=\frac{P \cos (\theta)}{\frac{A}{\sin (\theta)}}=\frac{P \sin (\theta) \cos (\theta)}{A}} \tag{2.4}\]
𝜎 = Average normal stress on the inclined plane [Pa, psi]
τ = Average shear stress on the inclined plane [Pa, psi]
N = Internal normal force perpendicular to the inclined plane [N, lb]
V = Internal shear force perpendicular to the inclined plane [N, lb]
Ap = Area of the inclined plane [m2, in.2]
A = Cross-sectional area [m2, in2]
P = Internal load perpendicular to cross-sectional area A [N, lb]
𝜃 = Angle between the inclined plane and the axis perpendicular to cross-sectional area A [°]
Note these equations assume the angle (𝜃) is measured from the axis perpendicular to area A. For a horizontal beam, area A is in the vertical plane so angle θ is measured from the horizontal axis.
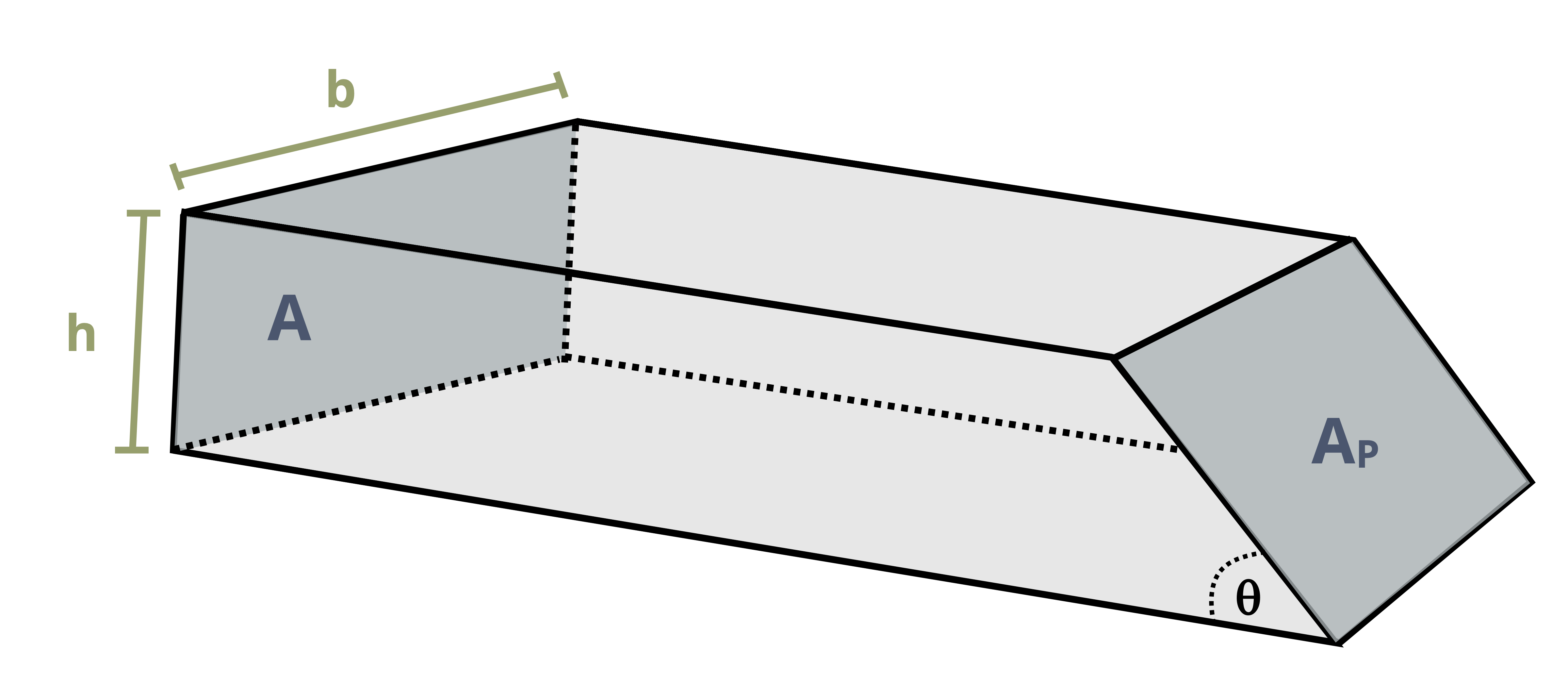
Even if the external load remains constant, we can obtain different values for the internal normal and shear forces (and therefore different values for the stresses) by changing the angle at which we cut the cross-section. We’ll explore the implications of this further in Chapter 12. For now, a demonstration of calculating the stresses on an inclined plane is given in Example 2.5.



.png)