13 Thin-Walled Pressure Vessels
Introduction
Click to expand
Pressure vessels are storage tanks that are used for storing fluids at high pressure and they must be designed to resist this pressure. They are commonly found in factories, power plants, vehicles, and even your own home. Figure 13.1 shows some common applications.
Pressure vessels are necessarily hollow, and a thin-walled pressure vessel is one where the ratio:
\[ \frac{\text { Inner radius }}{\text { Wall thickness }}>10 \]
This implies that the wall thickness is relatively small compared to the vessel radius. This simplifies our analysis in two ways:
- We can assume that stresses in the vessel walls are uniform across the thickness of the wall
- We can ignore stress in the radial direction (perpendicular to the vessel wall)
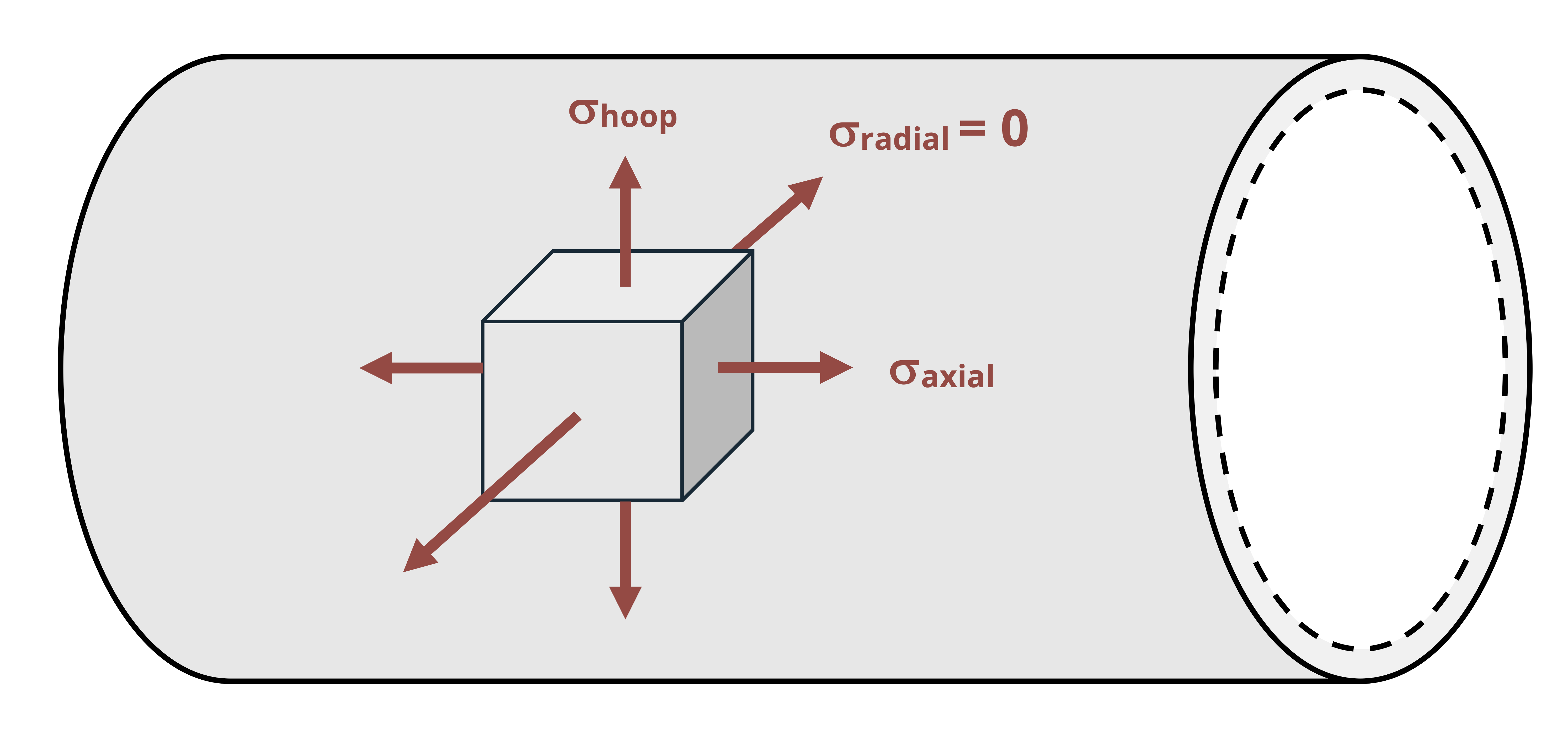
As weβll see in this chapter, stresses are generated in the walls of thin-walled pressure vessels in two directions known as the axial stress and hoop stress (Figure 13.2). There is a 3rd stress in the radial direction but this is very small compared to the other stresses and is assumed to be zero in this text.
As seen in Figure 13.1, thin-walled pressure vessels are commonly either cylindrical or spherical. Section 13.1 will discuss the stresses in cylindrical vessels. Section 13.2 will discuss the stresses in spherical vessels.
13.1 Cylindrical Pressure Vessels
Click to expand
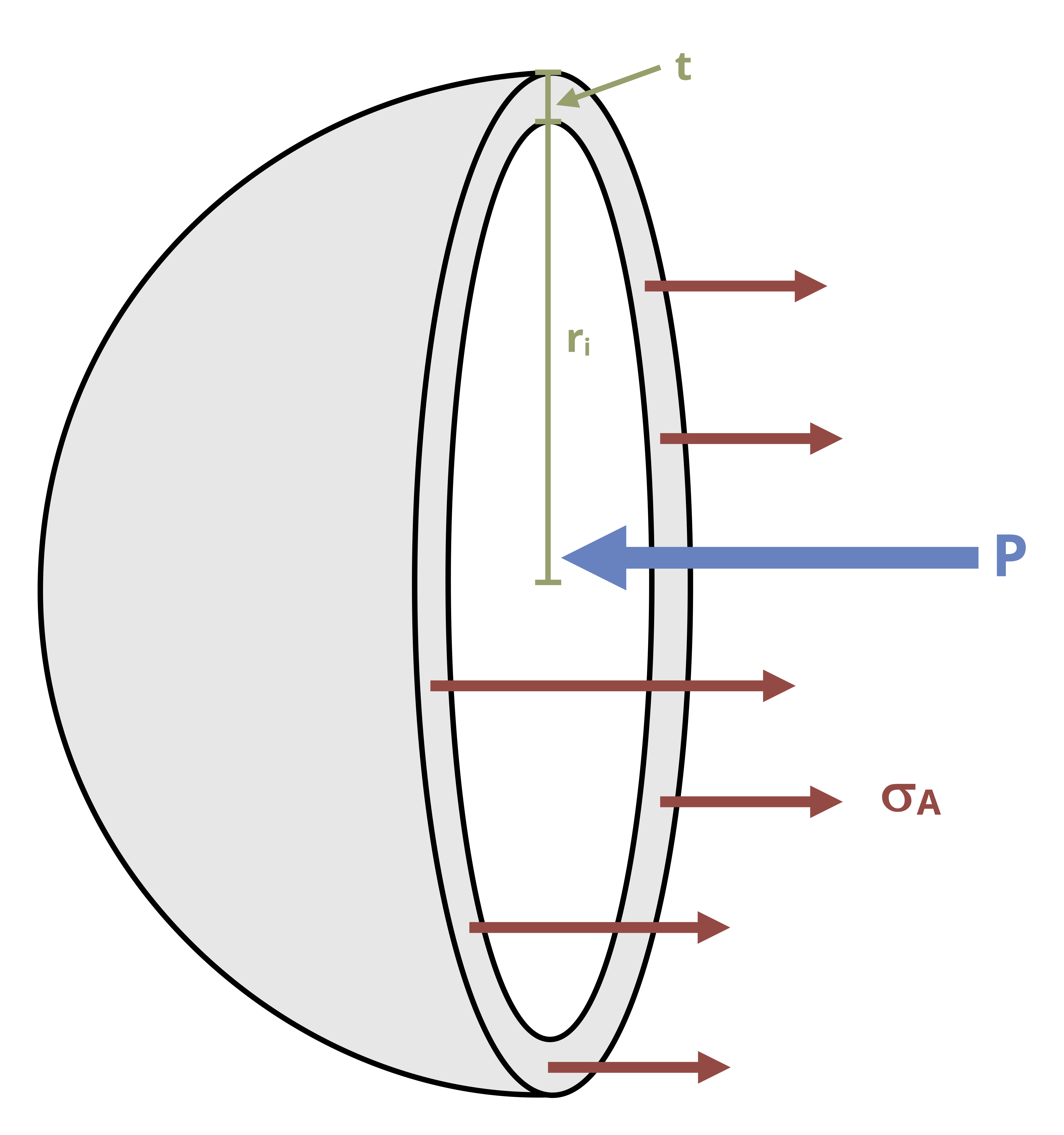
The equations stresses in the wall of a cylindrical pressure vessel can be derived with the help of a free body diagram. Letβs cut a cross-section through our vessel to expose the fluid inside (Figure 13.3).
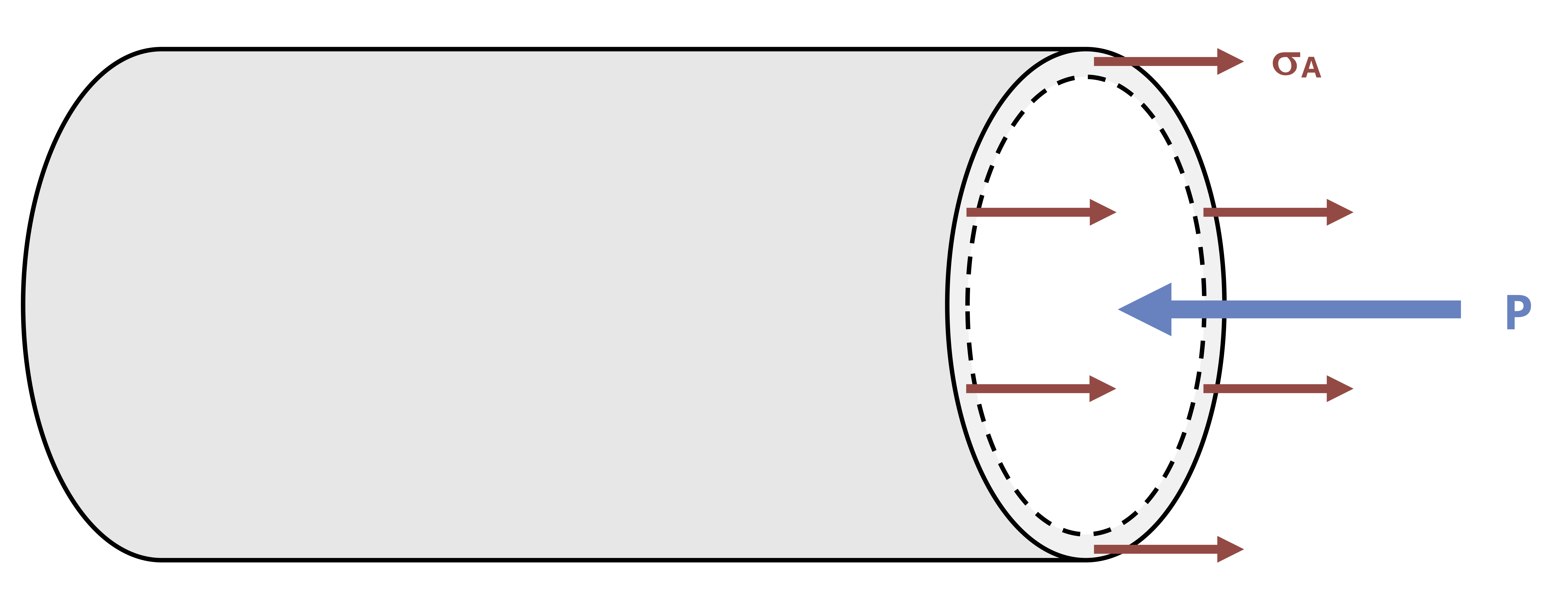
There will be an axial stress from the internal fluid pressure (P) and an axial stress in the walls of the vessel (ππ΄). Since \(\text{stress}=\frac{\text { force }}{\text { area }}\) we can determine the two forces. The fluid pressure acts over a circular area \(A=\pi r_i^2\). The stress in the walls acts over an area equal to the circumference of the vessel multiplied by the wall thickness, \(A=2 \pi r_i t\).
By equilibrium:
\[ \sum F_x=\left(\sigma_A\right)\left(2 \pi r_i t\right)-(P)\left(\pi r_i^2\right)=0 \\ \]
\[ \boxed{\sigma_A=\frac{P r_i}{2 t}} \tag{13.1}\]
ππ΄ = Axial stress in the wall of the vessel [Pa, psi]
P = Fluid pressure inside the vessel [Pa, psi]
ri = Inner radius of the vessel [m, in.]
t = Wall thickness of the vessel [m, in.]
Similarly there will be a stress in the lateral direction, referred to as the hoop stress πH. Letβs cut a vertical cross-section (Figure 13.4) to derive an equation for this stress.
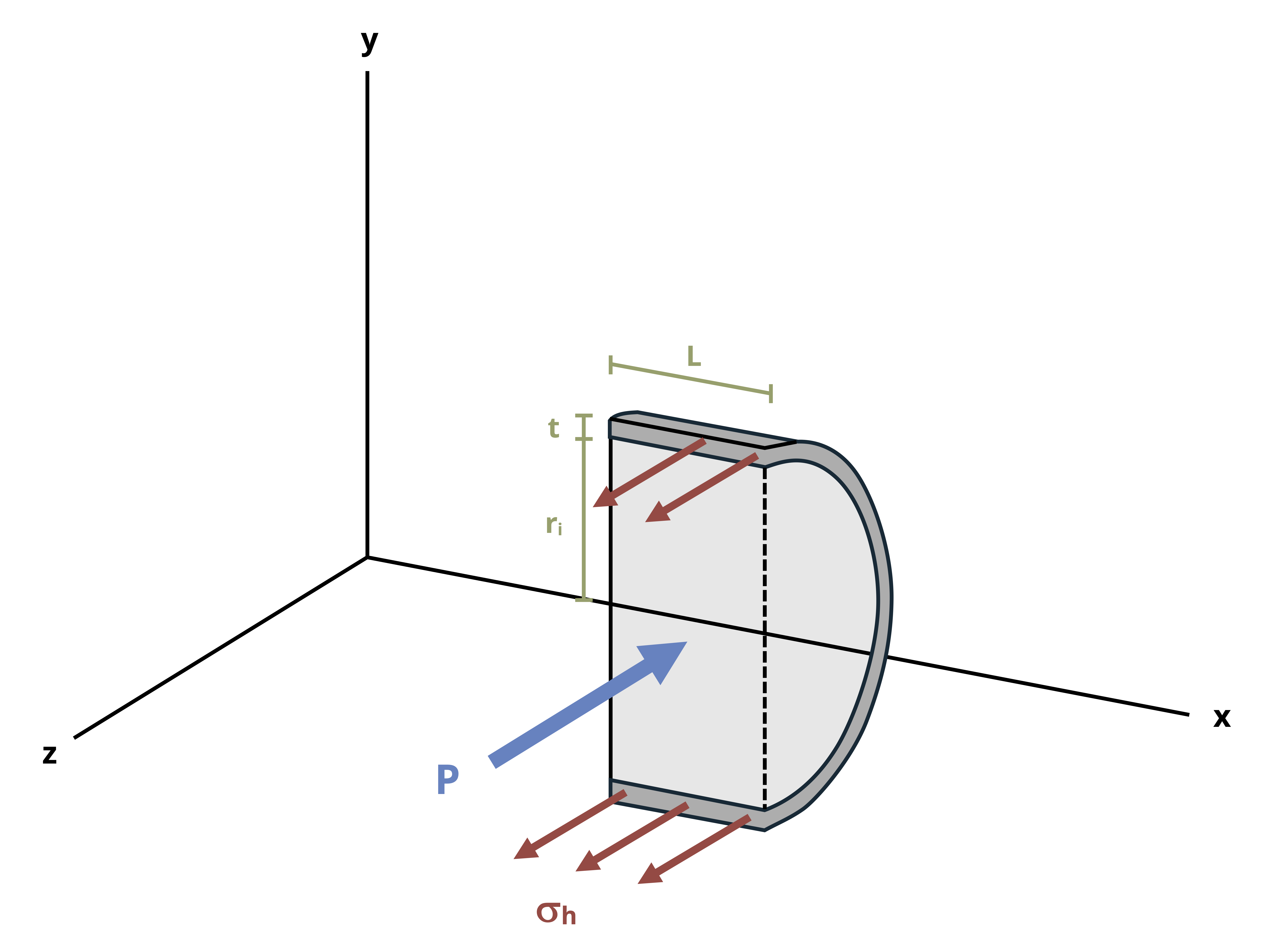
There will again be a stress from the internal fluid pressure (P) and a stress in the walls of the vessel (πH). The fluid pressure acts over an area of \(A=2 r_i L\). The stress in the walls acts over an area of \(A=2 t L\).
By equilibrium:
\[ \sum F_x=\left(\sigma_H\right)(2 t L)-(P)\left(2 r_i L\right)=0 \\ \]
\[ \boxed{\sigma_H=\frac{P r_i}{t}} \tag{13.2}\]
πH = Hoop stress in the wall of the vessel [Pa, psi]
P = Fluid pressure inside the vessel [Pa, psi]
ri = Inner radius of the vessel [m, in.]
t = Wall thickness of the vessel [m, in.]
The internal pressure P is typically reported as the gage pressure, which is defined as the internal pressure minus the atmospheric pressure. This allows us to calculate the stresses directly without needing to account for atmospheric pressure.
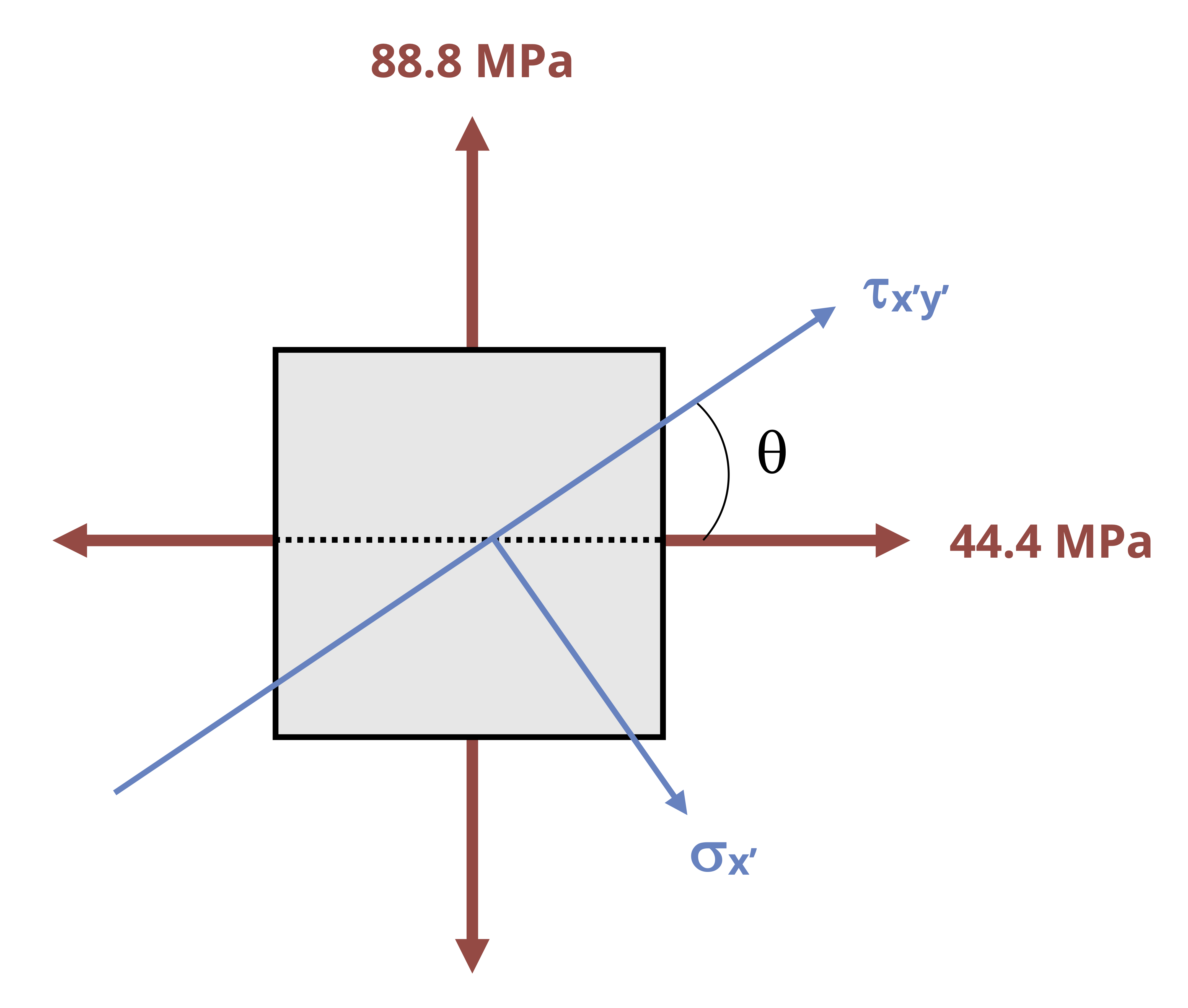
Since the radial stress is assumed to be zero, the axial and hoop stresses represent a state of plane stress such as those discussed in Chapter 12. Further, since there is no shear stress, the axial and hoop stresses represent the principal stresses. Since the hoop stress is larger, this is the first principal stress (π1). The axial stress is the second principal stress (π2). The third principal stress acts in the radial direction and has already been assumed to be zero. Figure 13.5 shows a plane stress element representing the stresses in the wall of a cylindrical thin-walled pressure vessel.
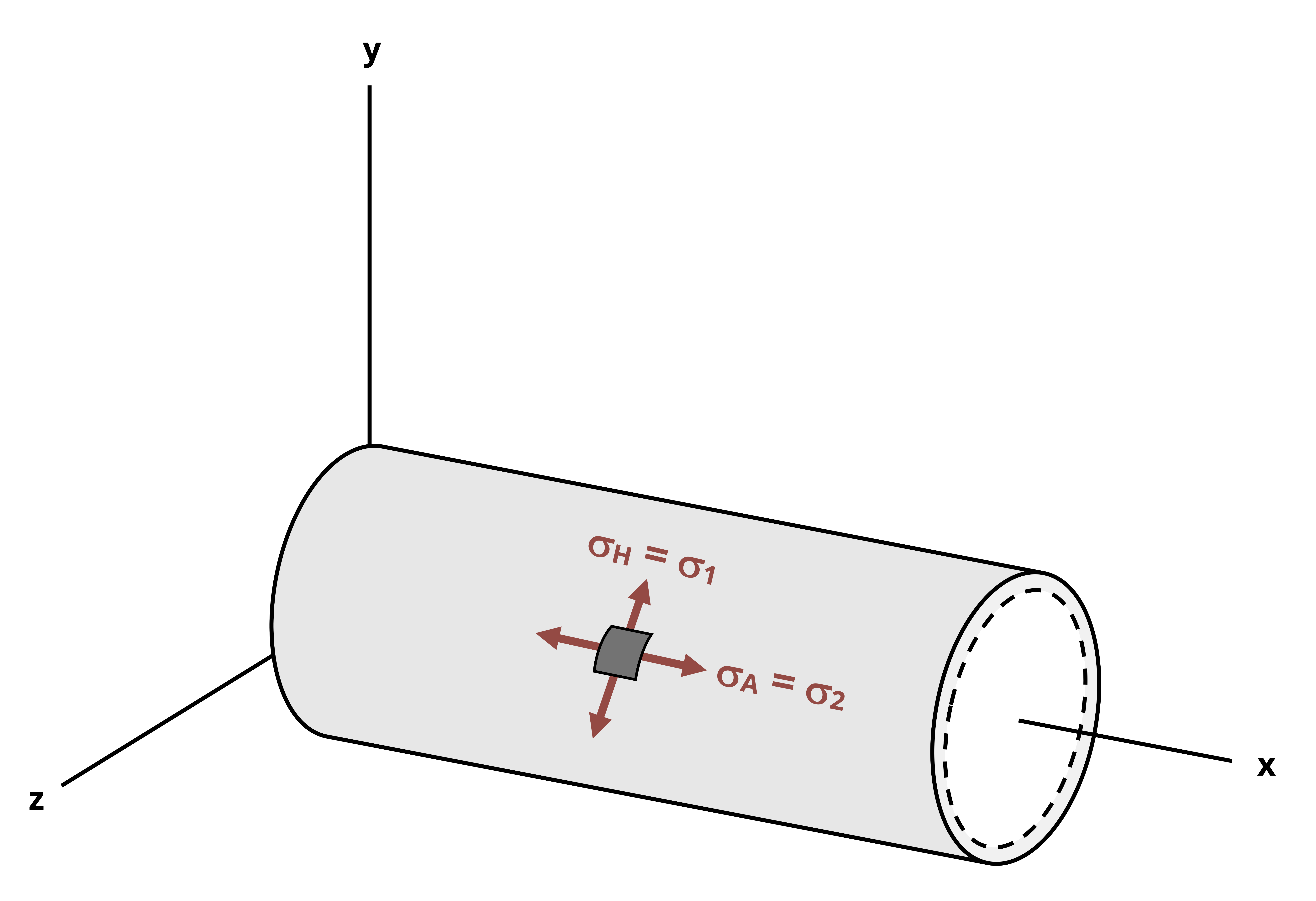
By the methods of Chapter 12 we may perform stress transformation on these stresses. Figure 13.6 shows Mohrβs Circle for the in-plane and out-of-plane stresses.
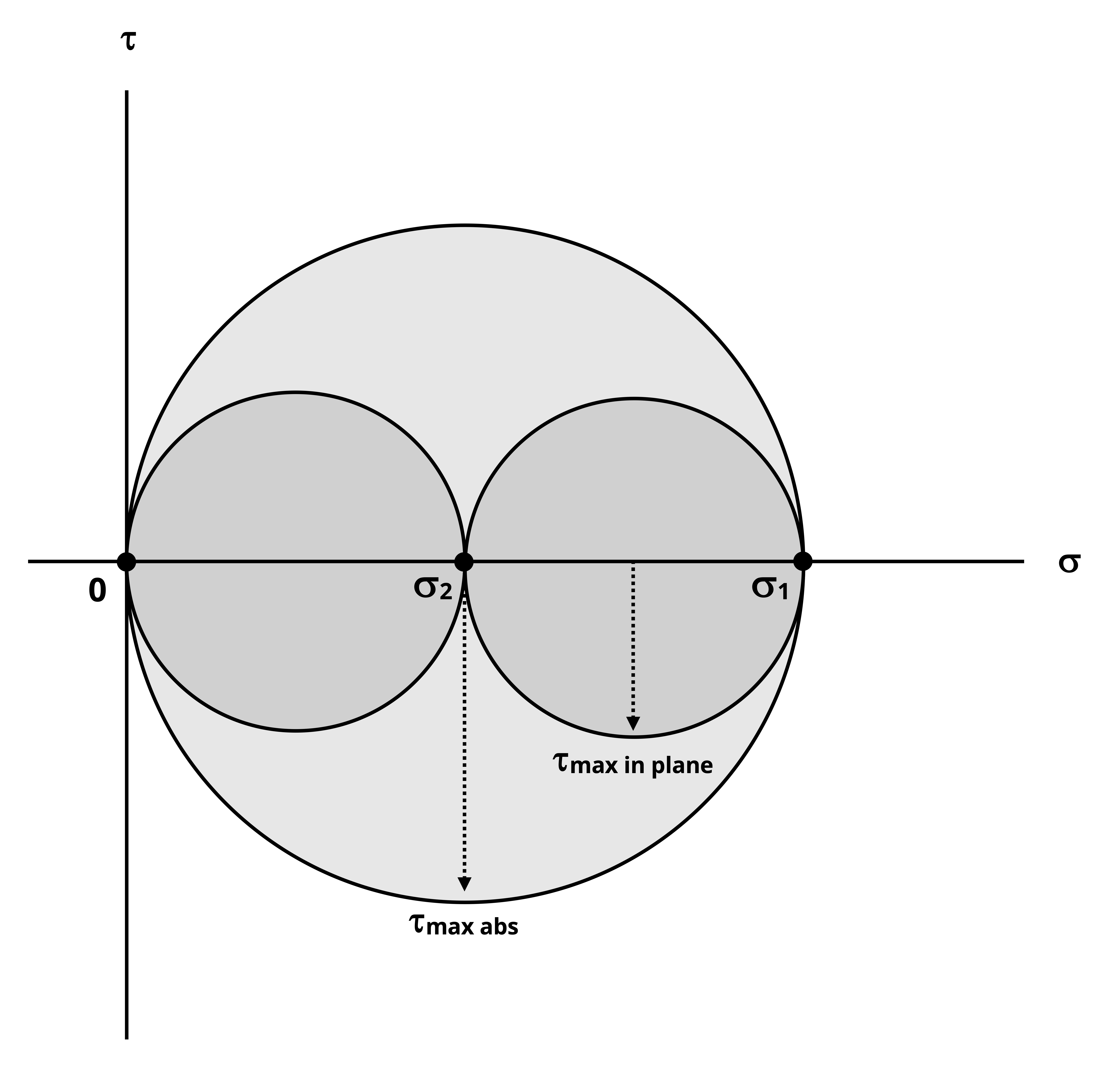
Since the two principal stresses are positive and the third principal stress is zero it should be apparent that the maximum in plane shear stress can be determined as:
\[ \tau_{max~in~plane}=\frac{\sigma_1-\sigma_2}{2} \]
It should also be apparent that the maximum out-of-plane shear stress will be larger and can be calculated from:
\[ \tau_{\max a b s}=\frac{\sigma_1}{2} \]
Example 13.1 demonstrates calculation of the principal stresses and maximum in-plane shear stress for a cylindrical thin-walled pressure vessel. Example 13.2 combine the content from this section with stress transformation from Chapter 12 in order to find the stresses at specific orientations.
Example 13.2
A cylindrical pressure vessel is made by welding steel plate at an angle of π=25Β° as shown. The vessel has an outer diameter of 1.5 m and a wall thickness of 40 mm. The vessel contains fluid at a gage pressure of 5 MPa. Determine the normal stress perpendicular to the weld and the shear stress parallel to the weld.
First determine the inner radius of the vessel. Wall thickness π‘ = 40 ππ = 0.04 π.
Outer radius, \(r_o = \frac{1.5{~m}}{2} =0.75{~m}\)
Inner radius, \(r_i = 0.75{~m} - 0.04{~m} = 0.71{~m}\)
Now calculate the axial and hoop stresses.
\[ \begin{aligned} & \sigma_A=\frac{Pr_i}{2t}=\frac{5{~MPa} * 0.71{~m}}{2 * 0.04{~m}}=44.4{~MPa} \\ & \sigma_H=\frac{Pr_i}{t}=\frac{5{~MPa} * 0.71{`m}}{0.04{~m}}=88.8{~MPa} \end{aligned} \]
By the methods of Section 12.1 we can calculate the normal stress perpendicular to the weld. Draw a stress element of a point on the pressure vessel. The axial stress will act horizontally and the hoop stress vertically for this element.
The weld is at an angle of 25Β° measured counter-clockwise from horizontal. The normal stress perpendicular to this weld is therefore at an angle of 65Β° clockwise from horizontal. We can determine the normal stress at this orientation from:
\[ \begin{gathered} \sigma_x^{\prime}=\frac{\sigma_x+\sigma_y}{2}+\frac{\sigma_x-\sigma_y}{2} \cos (2 \theta)+\tau_{x y} \sin (2 \theta) \\ \sigma_x^{\prime}=\frac{44.4{~MPa}+88.8{~MPa}}{2}+\frac{44.4{~MPa}-88.8{~MPa}}{2} \cos \left(2 *-65^{\circ}\right)+0 \\ \sigma_x^{\prime}=66.6{~MPa}-22.2{~MPa}*\cos \left(-130^{\circ}\right) \\ \sigma_x^{\prime}=80.9{~MPa} \end{gathered} \]
The shear stress occurs parallel to the weld at an angle of 25Β° counter-clockwise from the horizontal. We can determine the shear stress at this orientation from:
\[ \begin{gathered} \tau_{x^{\prime} y^{\prime}}=-\left(\frac{\sigma_x-\sigma_y}{2}\right) \sin (2 \theta)+\tau_{x y} \cos (2 \theta) \\ \tau_{x^{\prime} y^{\prime}}=-\left(\frac{44.4{~MPa}-88.8{~MPa}}{2}\right) \sin \left(2 * 25^{\circ}\right)+0 \\ \tau_{x^{\prime} y^{\prime}}=-\left(\frac{44.4{~MPa}-88.8{~MPa}}{2}\right) \sin \left(2 * 25^{\circ}\right)+0 \\ \tau_{x^{\prime} y^{\prime}}=22.2{~MPa}* \sin \left(50^{\circ}\right) \\ \tau_{x^{\prime} y^{\prime}}=17.0{~MPa} \end{gathered} \]
13.2 Spherical Pressure Vessels
Click to expand
A spherical vessel will yield the same cross-section regardless of the axis it is cut along (Figure 13.7). The stress in the walls of a spherical vessel is the same as the axial stress in a cylindrical vessel.
By equilibrium:
\[ \sum F_x=\left(\sigma_A\right)\left(2 \pi r_i t\right)-(P)\left(\pi r_i^2\right)=0 \]
\[ \boxed{\sigma_A=\frac{P r_i}{2 t}} \tag{13.3}\]
πA = Axial stress in the wall of the vessel [Pa, psi]
P = Fluid pressure inside the vessel [Pa, psi]
ri = Inner radius of the vessel [m, in.]
t = Wall thickness of the vessel [m, in.]
In this case, the same stress exists in both principal directions. We will again assume that the radial stress is zero, meaning that these stresses again form a state of plane stress (Figure 13.8). There is again no shear stress, so these stresses are the principal stresses. In this case, the two principal stresses are the same.
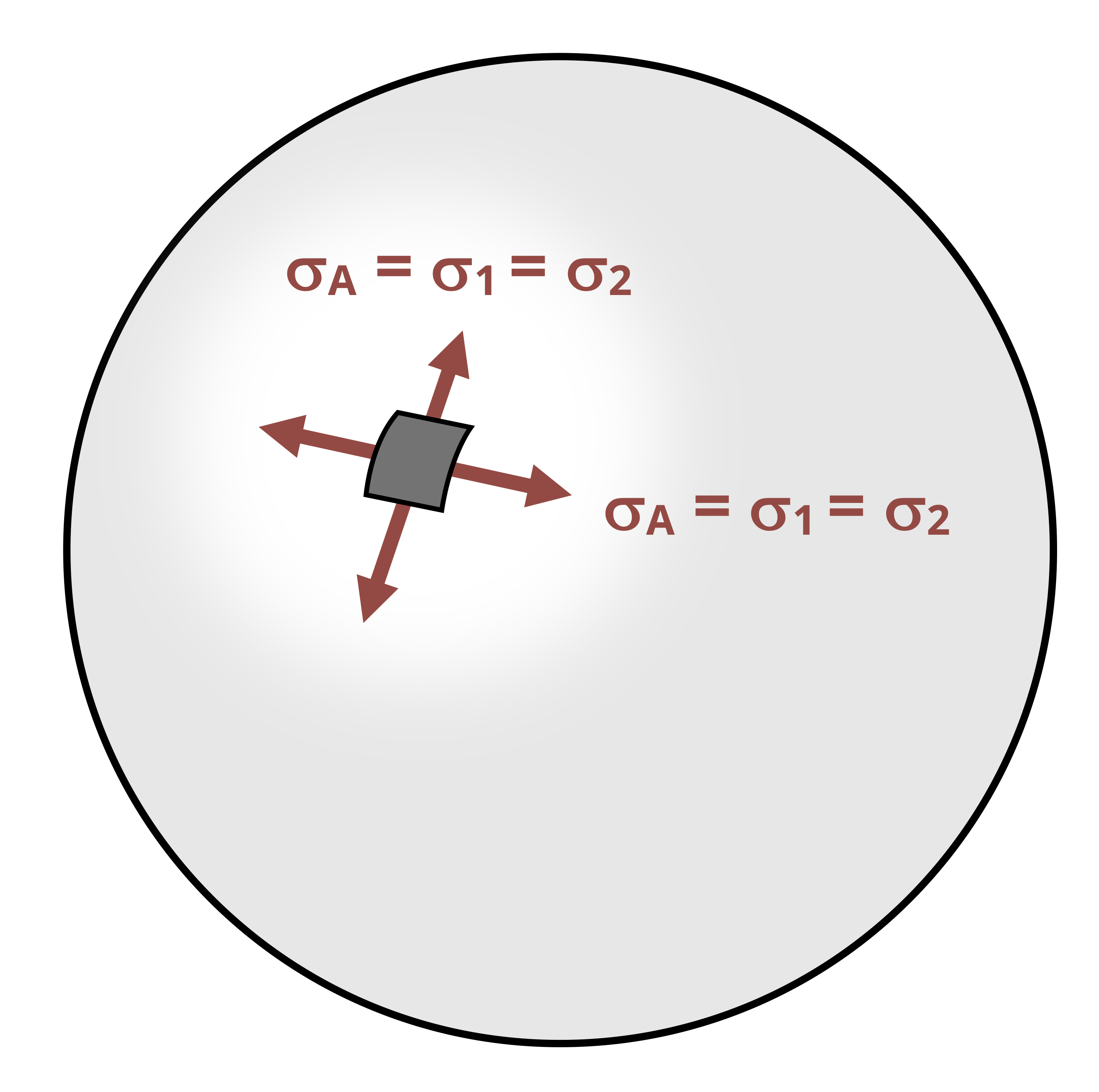
Note that these principal stresses are equal to π2 in the cylindrical vessel. As such, spherical vessels are stronger than cylindrical vessels. However, they are also more expensive to manufacture so cylindrical vessels are still very common.
We may again use the methods of Chapter 12 to perform stress transformation. Figure 13.9 shows Mohrβs Circle for the in-plane and out-of-plane stresses.
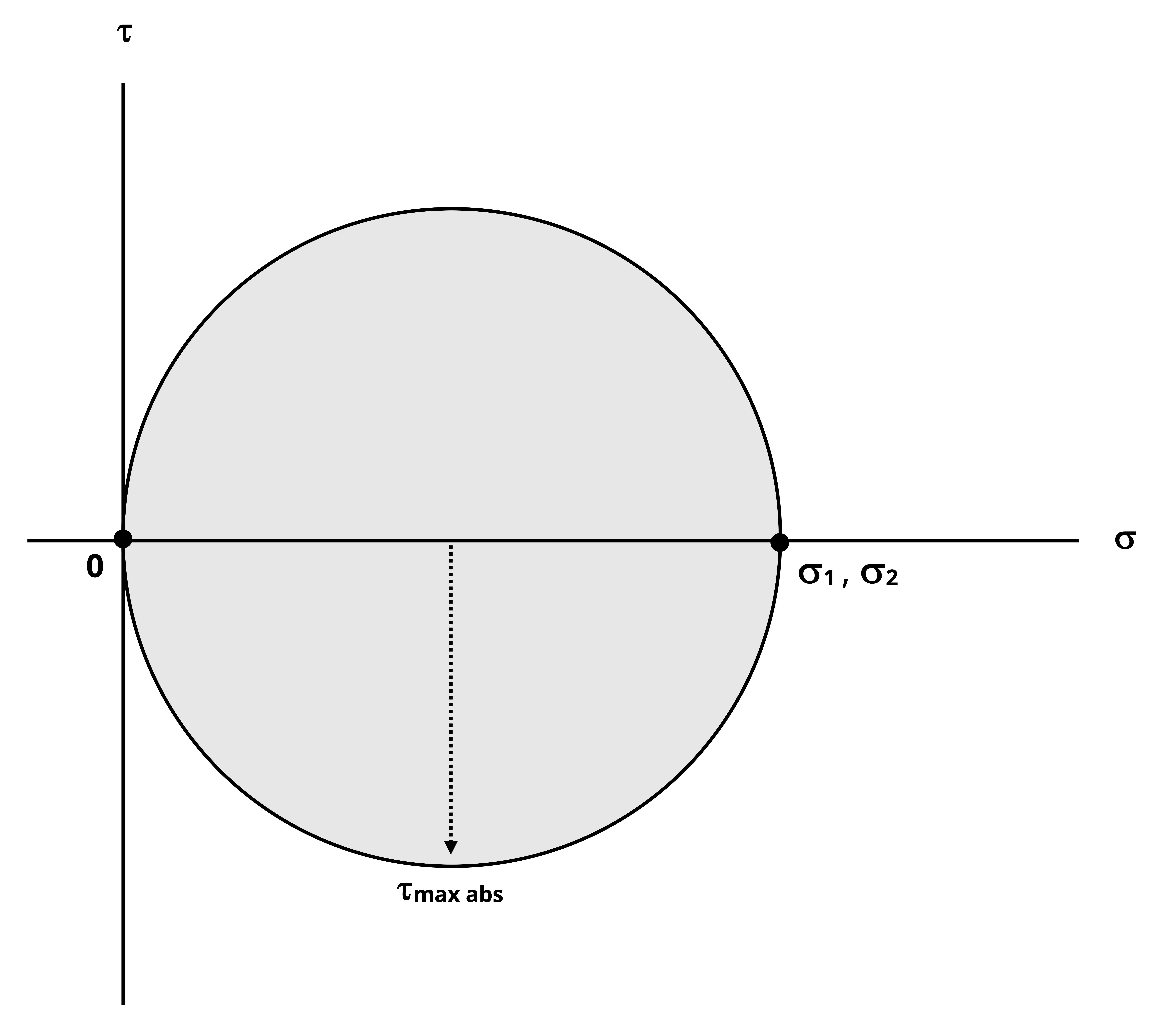
This time π1 = π2 and so the in-plane Mohrβs Circle reduces to a single point. The maximum in-plane shear stress is therefore zero. The maximum out-of-plane shear stress can be calculated from:
\[ \tau_{\max a b s}=\frac{\sigma_1}{2} \]
Example 13.3 demonstrates the design of a spherical vessel, based on the allowable stress in the vessel walls.